
We can also calculate the Standard Deviation of the distribution of sample means.
This mean would equal the true population mean. We could then calculate an average of all of our sample means. If we were to draw an infinite number of samples (of equal size) from our population, we could display the observed means as a distribution. If the mean value for a rating attribute was 3.2 for one sample, it might be 3.4 for a second sample of the same size. If a second sample was drawn, the results probably won't exactly match the first sample. We then make inferences about the population from the results obtained from that sample. Most survey research involves drawing a sample from a population. A larger sample size will normally result in a smaller SE (while SD is not directly affected by sample size). A small SE is an indication that the sample mean is a more accurate reflection of the actual population mean. The Standard Error ("Std Err" or "SE"), is an indication of the reliability of the mean.
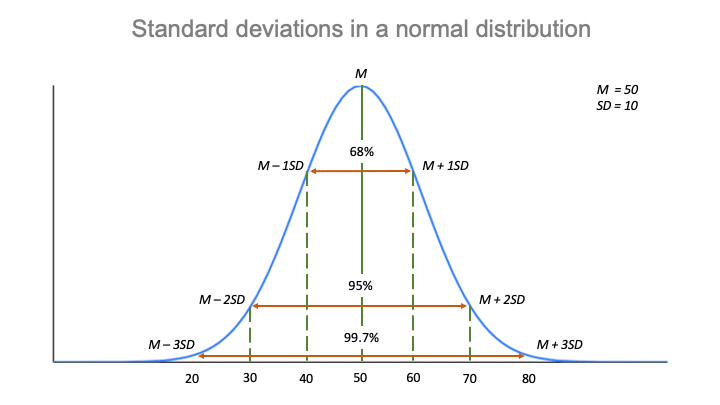
More important is to understand what the statistics convey. Most tabulation programs, spreadsheets or other data management tools will calculate the SD for you. For practical purposes, the computation is not important. Instead, it is "standardized," a somewhat complex method of computing the value using the sum of the squares. However, it is not actually calculated as an average (if it were, we would call it the "average deviation"). *Technical disclaimer: thinking of the Standard Deviation as an "average deviation" is an excellent way of conceptionally understanding its meaning. It describes the distribution in relation to the mean. It is used purely as a descriptive statistic. SD generally does not indicate "right or wrong" or "better or worse" - a lower SD is not necessarily more desireable. A distribution with a low SD would display as a tall narrow shape, while a large SD would be indicated by a wider shape. Respondent:Īnother way of looking at Standard Deviation is by plotting the distribution as a histogram of responses. The Standard Deviation of 1.15 shows that the individual responses, on average*, were a little over 1 point away from the mean. In Rating "B", even though the group mean is the same (3.0) as the first distribution, the Standard Deviation is higher. The individual responses did not deviate at all from the mean. In the first example (Rating "A") the Standard Deviation is zero because ALL responses were exactly the mean value. Consider the following example showing response values for two different ratings. Two very different distributions of responses to a 5-point rating scale can yield the same mean. The distribution of responses is important to consider and the SD provides a valuable descriptive measure of this. Looking at the mean alone tells only part of the story, yet all too often, this is what researchers focus on. But the higher SD for reliability could indicate (as shown in the distribution below) that responses were very polarized, where most respondents had no reliability issues (rated the attribute a "5"), but a smaller, but important segment of respondents, had a reliability problem and rated the attribute "1". At first glance (looking at the means only) it would seem that reliability was rated higher than value.

The mean for a group of ten respondents (labeled 'A' through 'J' below) for "good value for the money" was 3.2 with a SD of 0.4 and the mean for "product reliability" was 3.4 with a SD of 2.1.
Midpoints less accurate standard deviation series#
Let's say you've asked respondents to rate your product on a series of attributes on a 5-point scale. SD tells the researcher how spread out the responses are - are they concentrated around the mean, or scattered far & wide? Did all of your respondents rate your product in the middle of your scale, or did some love it and some hate it? Standard Deviation (often abbreviated as "Std Dev" or "SD") provides an indication of how far the individual responses to a question vary or "deviate" from the mean. They are often referred to as the "standard deviation of the mean" and the "standard error of the mean." However, they are not interchangeable and represent very different concepts. Both statistics are typically shown with the mean of a variable, and in a sense, they both speak about the mean. The following article is intended to explain their meaning and provide additional insight on how they are used in data analysis. Standard Deviation and Standard Error are perhaps the two least understood statistics commonly shown in data tables.


 0 kommentar(er)
0 kommentar(er)
